Chi-square Test

Following are the 2 types of Chi-square test:

• Chi-square test of independence
• Chi-square goodness of fit (This is used to test whether a sample data correctly represent a population data)

Chi-square test of independence

This is used to determine if there is a significant relationship between 2 nominal (categorical) variables.

For example, a researcher wants to examine the relationship between gender (male vs female) and chances of getting Alzheimer’s disease. The chi-square test of independence can be used to examine this relationship.

• The null hypothesis ($H_0$) for this test is that there is no relationship between gender and life expectancy, and
• The alternative hypothesis is that there is a relationship between gender and empathy.

Here, there are two categorical variables (nominal variables) — male and female.

The expected value is calculated by assuming that the null hypothesis is correct. So, if you select a sample of, say, 100 Alzheimer’s patients, 50 should be men and 50 should be women.

Let’s say the sample value comes up to be a bit different, and in a sample of 100 Alzheimer’s patients, 60 are men and 40 are women.

Let’s draw a table for both these categorical values:

_	Male	Female
Expected value	50	50
Sample value	60	40

The test-statistic for Chi-square test is:

$$\chi^2 = \sum{\dfrac{(O - E)^2}{E}}$$

where,

• O is the observed sample value
• E is the Expected value

So, our test statstic would be

$$\chi^2 = (10^2)/50 + (10^2)/50 = 4$$

Let’s select the level of significance as 5%, or 0.05.
Degrees of freedom $= (r-1) \cdot (c-1)$, where r is the number of rows and c is the number of columns.

So, the degree of freedom in this case is 1.

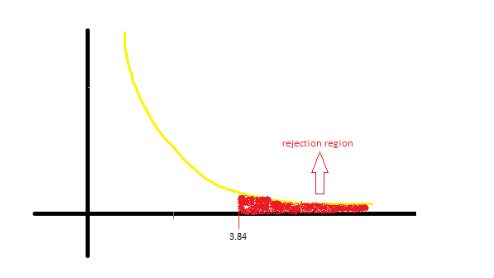
Now, you will use the chi-square distribution table) to calculate the critical value.

Select the value corresponding to the required Degrees of freedom and the significance level.

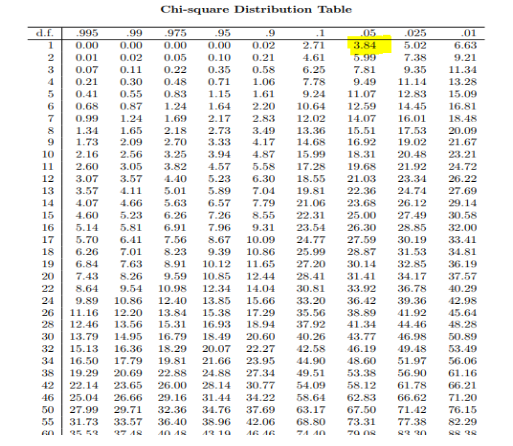
So, the critical value is 3.84, and the test statistic value is 4.

In this case, the test statistic value (4), which is greater than the critical value, lies in the rejection region. Therefore, you fail to accept the null hypothesis.